Draw Circle Between Two Points

Skip to main content

Three Ways to Describe an Arc

• Commodity
• 07/08/2021
• 16 minutes to read

Is this folio helpful?

Feedback will be sent to Microsoft: By pressing the submit push, your feedback will be used to ameliorate Microsoft products and services. Privacy policy.

In this article

Download the sample

Learn how to use SkiaSharp to define arcs in three different ways

An arc is a curve on the circumference of an ellipse, such as the rounded parts of this infinity sign:

Despite the simplicity of that definition, in that location is no way to define an arc-drawing function that satisfies every demand, and hence, no consensus among graphics systems of the best way to draw an arc. For this reason, the SKPath class does non restrict itself to merely i approach.

SKPath defines an AddArc method, five different ArcTo methods, and two relative RArcTo methods. These methods fall into iii categories, representing three very different approaches to specifying an arc. Which 1 you use depends on the information available to define the arc, and how this arc fits in with the other graphics that y'all're drawing.

The Bending Arc

The angle arc approach to drawing arcs requires that you specify a rectangle that bounds an ellipse. The arc on the circumference of this ellipse is indicated by angles from the centre of the ellipse that indicate the beginning of the arc and its length. Two different methods draw bending arcs. These are the AddArc method and the ArcTo method:

              public void AddArc (SKRect oval, Unmarried startAngle, Unmarried sweepAngle)  public void ArcTo (SKRect oval, Single startAngle, Single sweepAngle, Boolean forceMoveTo)                          

These methods are identical to the Android AddArc and [ArcTo]xref:Android.Graphics.Path.ArcTo*) methods. The iOS AddArc method is similar merely is restricted to arcs on the circumference of a circumvolve rather than generalized to an ellipse.

Both methods brainstorm with an SKRect value that defines both the location and size of an ellipse:

The arc is a part of the circumference of this ellipse.

The startAngle argument is a clockwise angle in degrees relative to a horizontal line fatigued from the center of the ellipse to the right. The sweepAngle argument is relative to the startAngle. Here are startAngle and sweepAngle values of 60 degrees and 100 degrees, respectively:

The arc begins at the offset angle. Its length is governed past the sweep angle. The arc is shown hither in scarlet:

The curve added to the path with the AddArc or ArcTo method is simply that office of the ellipse'due south circumference:

The startAngle or sweepAngle arguments can be negative: The arc is clockwise for positive values of sweepAngle and counter-clockwise for negative values.

Withal, AddArc does not define a closed contour. If y'all call LineTo subsequently AddArc, a line is drawn from the end of the arc to the point in the LineTo method, and the same is true of ArcTo.

AddArc automatically starts a new contour and is functionally equivalent to a telephone call to ArcTo with a final argument of true:

              path.ArcTo (oval, startAngle, sweepAngle, true);                          

That concluding argument is called forceMoveTo, and information technology effectively causes a MoveTo call at the beginning of the arc. That begins a new contour. That is not the case with a last argument of simulated:

              path.ArcTo (oval, startAngle, sweepAngle, false);                          

This version of ArcTo draws a line from the electric current position to the outset of the arc. This means that the arc can be somewhere in the heart of a larger contour.

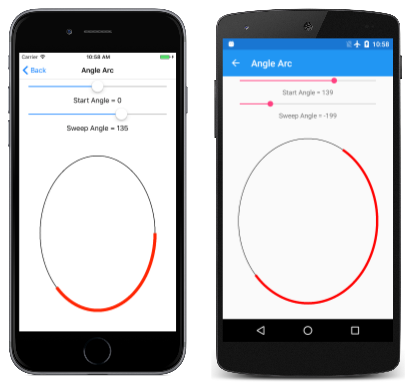
The Angle Arc page lets you use two sliders to specify the kickoff and sweep angles. The XAML file instantiates two Slider elements and an SKCanvasView. The PaintCanvas handler in the AngleArcPage.xaml.cs file draws both the oval and the arc using two SKPaint objects divers as fields:

              void OnCanvasViewPaintSurface(object sender, SKPaintSurfaceEventArgs args) {     SKImageInfo info = args.Info;     SKSurface surface = args.Surface;     SKCanvas canvas = surface.Canvas;      sheet.Articulate();      SKRect rect = new SKRect(100, 100, info.Width - 100, info.Height - 100);     float startAngle = (float)startAngleSlider.Value;     float sweepAngle = (float)sweepAngleSlider.Value;      canvas.DrawOval(rect, outlinePaint);      using (SKPath path = new SKPath())     {         path.AddArc(rect, startAngle, sweepAngle);         canvas.DrawPath(path, arcPaint);     } }                          

As you can see, both the start angle and the sweep angle can take on negative values:

This approach to generating an arc is algorithmically the simplest, and it's easy to derive the parametric equations that describe the arc. Knowing the size and location of the ellipse, and the start and sweep angles, the start and end points of the arc can be calculated using simple trigonometry:

ten = oval.MidX + (oval.Width / two) * cos(angle)

y = oval.MidY + (oval.Height / 2) * sin(angle)

The bending value is either startAngle or startAngle + sweepAngle.

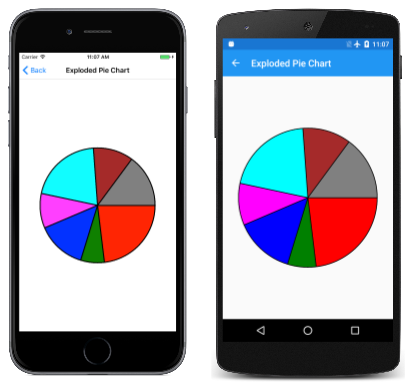
The use of two angles to define an arc is best for cases where you know the angular length of the arc that you want to describe, for case, to make a pie nautical chart. The Exploded Pie Nautical chart page demonstrates this. The ExplodedPieChartPage class uses an internal course to define some fabricated data and colors:

              grade ChartData {     public ChartData(int value, SKColor color)     {         Value = value;         Color = color;     }      public int Value { individual prepare; get; }      public SKColor Color { private set; get; } }  ChartData[] chartData = {     new ChartData(45, SKColors.Red),     new ChartData(13, SKColors.Green),     new ChartData(27, SKColors.Blue),     new ChartData(19, SKColors.Magenta),     new ChartData(40, SKColors.Cyan),     new ChartData(22, SKColors.Brown),     new ChartData(29, SKColors.Greyness) };                          

The PaintSurface handler first loops through the items to calculate a totalValues number. From that, it can determine each detail's size as the fraction of the total, and convert that to an bending:

              void OnCanvasViewPaintSurface(object sender, SKPaintSurfaceEventArgs args) {     SKImageInfo info = args.Info;     SKSurface surface = args.Surface;     SKCanvas sheet = surface.Canvas;      canvas.Clear();      int totalValues = 0;      foreach (ChartData item in chartData)     {         totalValues += detail.Value;     }      SKPoint center = new SKPoint(info.Width / 2, info.Height / two);     float explodeOffset = 50;     bladder radius = Math.Min(info.Width / 2, info.Height / 2) - 2 * explodeOffset;     SKRect rect = new SKRect(center.10 - radius, center.Y - radius,                              center.X + radius, center.Y + radius);      float startAngle = 0;      foreach (ChartData particular in chartData)     {         bladder sweepAngle = 360f * particular.Value / totalValues;          using (SKPath path = new SKPath())         using (SKPaint fillPaint = new SKPaint())         using (SKPaint outlinePaint = new SKPaint())         {             path.MoveTo(center);             path.ArcTo(rect, startAngle, sweepAngle, false);             path.Close();              fillPaint.Style = SKPaintStyle.Fill;             fillPaint.Colour = item.Color;              outlinePaint.Style = SKPaintStyle.Stroke;             outlinePaint.StrokeWidth = 5;             outlinePaint.Color = SKColors.Black;              // Calculate "explode" transform             float angle = startAngle + 0.5f * sweepAngle;             float x = explodeOffset * (float)Math.Cos(Math.PI * bending / 180);             float y = explodeOffset * (float)Math.Sin(Math.PI * angle / 180);              canvass.Save();             sheet.Translate(x, y);              // Fill and stroke the path             canvas.DrawPath(path, fillPaint);             canvass.DrawPath(path, outlinePaint);             canvas.Restore();         }          startAngle += sweepAngle;     } }                          

A new SKPath object is created for each pie piece. The path consists of a line from the middle, then an ArcTo to describe the arc, and some other line back to the center results from the Shut call. This program displays "exploded" pie slices past moving them all out from the centre by 50 pixels. That task requires a vector in the direction of the midpoint of the sweep bending for each slice:

To see what information technology looks like without the "explosion," merely annotate out the Translate call:

The Tangent Arc

The 2nd type of arc supported by SKPath is the tangent arc, so chosen because the arc is the circumference of a circle that is tangent to two connected lines.

A tangent arc is added to a path with a telephone call to the ArcTo method with two SKPoint parameters, or the ArcTo overload with separate Single parameters for the points:

              public void ArcTo (SKPoint point1, SKPoint point2, Single radius)  public void ArcTo (Unmarried x1, Single y1, Unmarried x2, Unmarried y2, Unmarried radius)                          

This ArcTo method is similar to the PostScript arct (folio 532) role and the iOS AddArcToPoint method.

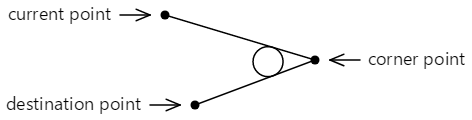
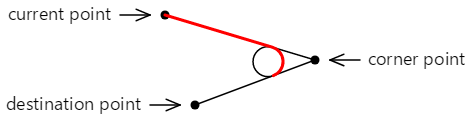
The ArcTo method involves three points:

• The current point of the contour, or the betoken (0, 0) if MoveTo has not been called
• The first betoken argument to the ArcTo method, chosen the corner point
• The second point argument to ArcTo, called the destination point:

These iii points define two continued lines:

If the three points are colinear — that is, if they lie on the same straight line — no arc volition be fatigued.

The ArcTo method also includes a radius parameter. This defines the radius of a circle:

The tangent arc is non generalized for an ellipse.

If the two lines see at any angle, that circle can be inserted between those lines so that information technology is tangent to both lines:

The curve that is added to the profile does not touch either of the points specified in the ArcTo method. It consists of a direct line from the current point to the first tangent point, and an arc that ends at the second tangent signal, shown here in ruby:

Here's the final direct line and arc that is added to the contour:

The profile tin be continued from the 2nd tangent point.

The Tangent Arc page allows you to experiment with the tangent arc. This is the start of several pages that derive from InteractivePage, which defines a few handy SKPaint objects and performs TouchPoint processing:

              public form InteractivePage : ContentPage {     protected SKCanvasView baseCanvasView;     protected TouchPoint[] touchPoints;      protected SKPaint strokePaint = new SKPaint     {         Style = SKPaintStyle.Stroke,         Color = SKColors.Black,         StrokeWidth = 3     };      protected SKPaint redStrokePaint = new SKPaint     {         Style = SKPaintStyle.Stroke,         Color = SKColors.Red,         StrokeWidth = 15     };      protected SKPaint dottedStrokePaint = new SKPaint     {         Fashion = SKPaintStyle.Stroke,         Colour = SKColors.Black,         StrokeWidth = 3,         PathEffect = SKPathEffect.CreateDash(new float[] { 7, 7 }, 0)     };      protected void OnTouchEffectAction(object sender, TouchActionEventArgs args)     {         bool touchPointMoved = false;          foreach (TouchPoint touchPoint in touchPoints)         {             float scale = baseCanvasView.CanvasSize.Width / (float)baseCanvasView.Width;             SKPoint indicate = new SKPoint(scale * (float)args.Location.10,                                         calibration * (float)args.Location.Y);             touchPointMoved |= touchPoint.ProcessTouchEvent(args.Id, args.Type, indicate);         }          if (touchPointMoved)         {             baseCanvasView.InvalidateSurface();         }     } }                          

The TangentArcPage form derives from InteractivePage. The constructor in the TangentArcPage.xaml.cs file is responsible for instantiating and initializing the touchPoints array, and setting baseCanvasView (in InteractivePage) to the SKCanvasView object instantiated in the TangentArcPage.xaml file:

              public partial class TangentArcPage : InteractivePage {     public TangentArcPage()     {         touchPoints = new TouchPoint[iii];          for (int i = 0; i < three; i++)         {             TouchPoint touchPoint = new TouchPoint             {                 Center = new SKPoint(i == 0 ? 100 : 500,                                      i != ii ? 100 : 500)             };             touchPoints[i] = touchPoint;         }          InitializeComponent();          baseCanvasView = canvasView;         radiusSlider.Value = 100;     }      void sliderValueChanged(object sender, ValueChangedEventArgs args)     {         if (canvasView != nothing)         {             canvasView.InvalidateSurface();         }     }     ... }                          

The PaintSurface handler uses the ArcTo method to draw the arc based on the touch points and a Slider, but also algorithmically calculates the circle that the bending is based on:

              public partial class TangentArcPage : InteractivePage {     ...     void OnCanvasViewPaintSurface(object sender, SKPaintSurfaceEventArgs args)     {         SKImageInfo info = args.Info;         SKSurface surface = args.Surface;         SKCanvas canvas = surface.Sheet;          sheet.Clear();          // Draw the two lines that meet at an angle         using (SKPath path = new SKPath())         {             path.MoveTo(touchPoints[0].Center);             path.LineTo(touchPoints[1].Center);             path.LineTo(touchPoints[2].Center);             sheet.DrawPath(path, dottedStrokePaint);         }          // Draw the circle that the arc wraps around         float radius = (bladder)radiusSlider.Value;          SKPoint v1 = Normalize(touchPoints[0].Heart - touchPoints[i].Heart);         SKPoint v2 = Normalize(touchPoints[2].Heart - touchPoints[ane].Middle);          double dotProduct = v1.Ten * v2.10 + v1.Y * v2.Y;         double angleBetween = Math.Acos(dotProduct);         float hypotenuse = radius / (float)Math.Sin(angleBetween / two);         SKPoint vMid = Normalize(new SKPoint((v1.Ten + v2.X) / 2, (v1.Y + v2.Y) / 2));         SKPoint center = new SKPoint(touchPoints[1].Center.X + vMid.Ten * hypotenuse,                                      touchPoints[1].Center.Y + vMid.Y * hypotenuse);          canvas.DrawCircle(middle.Ten, center.Y, radius, this.strokePaint);          // Draw the tangent arc         using (SKPath path = new SKPath())         {             path.MoveTo(touchPoints[0].Centre);             path.ArcTo(touchPoints[i].Center, touchPoints[two].Middle, radius);             sail.DrawPath(path, redStrokePaint);         }          foreach (TouchPoint touchPoint in touchPoints)         {             touchPoint.Paint(canvas);         }     }      // Vector methods     SKPoint Normalize(SKPoint v)     {         bladder magnitude = Magnitude(v);         return new SKPoint(v.X / magnitude, v.Y / magnitude);     }      float Magnitude(SKPoint v)     {         return (float)Math.Sqrt(v.X * v.X + v.Y * v.Y);     } }                          

Here's the Tangent Arc page running:

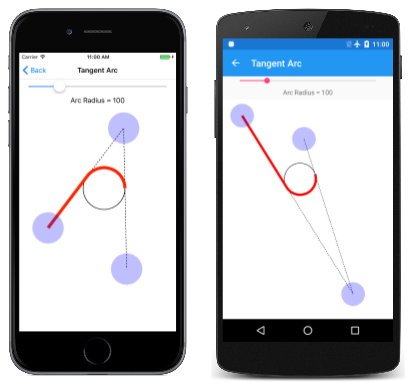
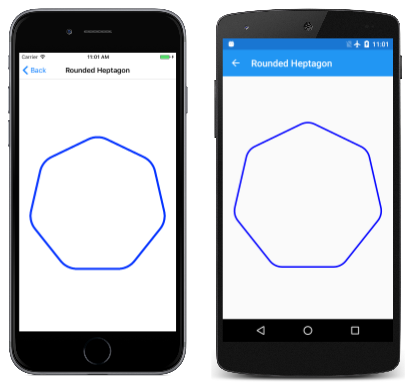
The tangent arc is platonic for creating rounded corners, such every bit a rounded rectangle. Considering SKPath already includes an AddRoundedRect method, the Rounded Heptagon page demonstrates how to use ArcTo for rounding the corners of a vii-sided polygon. (The code is generalized for any regular polygon.)

The PaintSurface handler of the RoundedHeptagonPage course contains one for loop to summate the coordinates of the seven vertices of the heptagon, and a second to calculate the midpoints of the seven sides from these vertices. These midpoints are then used to construct the path:

              void OnCanvasViewPaintSurface(object sender, SKPaintSurfaceEventArgs args) {     SKImageInfo info = args.Info;     SKSurface surface = args.Surface;     SKCanvas canvas = surface.Sail;      canvas.Clear();      float cornerRadius = 100;     int numVertices = 7;     bladder radius = 0.45f * Math.Min(info.Width, info.Tiptop);      SKPoint[] vertices = new SKPoint[numVertices];     SKPoint[] midPoints = new SKPoint[numVertices];      double vertexAngle = -0.5f * Math.PI;       // straight up      // Coordinates of the vertices of the polygon     for (int vertex = 0; vertex < numVertices; vertex++)     {         vertices[vertex] = new SKPoint(radius * (float)Math.Cos(vertexAngle),                                        radius * (bladder)Math.Sin(vertexAngle));         vertexAngle += 2 * Math.PI / numVertices;     }      // Coordinates of the midpoints of the sides connecting the vertices     for (int vertex = 0; vertex < numVertices; vertex++)     {         int prevVertex = (vertex + numVertices - one) % numVertices;         midPoints[vertex] = new SKPoint((vertices[prevVertex].10 + vertices[vertex].X) / ii,                                         (vertices[prevVertex].Y + vertices[vertex].Y) / 2);     }      // Create the path     using (SKPath path = new SKPath())     {         // Begin at the first midpoint         path.MoveTo(midPoints[0]);          for (int vertex = 0; vertex < numVertices; vertex++)         {             SKPoint nextMidPoint = midPoints[(vertex + 1) % numVertices];              // Draws a line from the electric current bespeak, and then the arc             path.ArcTo(vertices[vertex], nextMidPoint, cornerRadius);              // Connect the arc with the next midpoint             path.LineTo(nextMidPoint);         }         path.Shut();          // Render the path in the center of the screen         using (SKPaint pigment = new SKPaint())         {             paint.Style = SKPaintStyle.Stroke;             pigment.Color = SKColors.Blue;             paint.StrokeWidth = 10;              sheet.Translate(info.Width / 2, info.Tiptop / ii);             canvas.DrawPath(path, paint);         }     } }                          

Hither's the program running:

The Elliptical Arc

The elliptical arc is added to a path with a phone call to the ArcTo method that has two SKPoint parameters, or the ArcTo overload with dissever Ten and Y coordinates:

              public void ArcTo (SKPoint r, Single xAxisRotate, SKPathArcSize largeArc, SKPathDirection sweep, SKPoint xy)  public void ArcTo (Single rx, Single ry, Single xAxisRotate, SKPathArcSize largeArc, SKPathDirection sweep, Single x, Unmarried y)                          

The elliptical arc is consequent with the elliptical arc included in Scalable Vector Graphics (SVG) and the Universal Windows Platform ArcSegment class.

These ArcTo methods draw an arc betwixt two points, which are the electric current point of the profile, and the last parameter to the ArcTo method (the xy parameter or the separate 10 and y parameters):

The beginning point parameter to the ArcTo method (r, or rx and ry) is non a signal at all but instead specifies the horizontal and vertical radii of an ellipse;

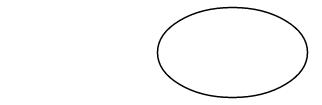
The xAxisRotate parameter is the number of clockwise degrees to rotate this ellipse:

If this tilted ellipse is and then positioned so that it touches the two points, the points are continued by two different arcs:

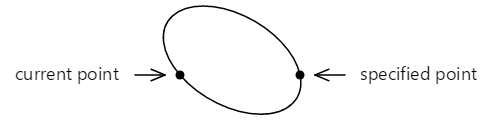
These two arcs tin can be distinguished in 2 ways: The top arc is larger than the bottom arc, and equally the arc is drawn from left to correct, the height arc is drawn in a clockwise direction while the bottom arc is drawn in a counter-clockwise direction.

It is as well possible to fit the ellipse between the two points in another mode:

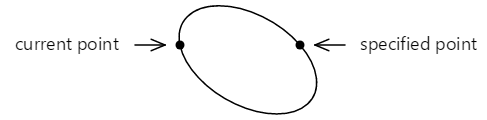
Now there'due south a smaller arc on top that'southward drawn clockwise, and a larger arc on the bottom that's fatigued counter-clockwise.

These 2 points tin therefore be connected past an arc defined past the tilted ellipse in a total of iv ways:

These four arcs are distinguished by the four combinations of the SKPathArcSize and SKPathDirection enumeration type arguments to the ArcTo method:

• red: SKPathArcSize.Large and SKPathDirection.Clockwise
• green: SKPathArcSize.Small and SKPathDirection.Clockwise
• blueish: SKPathArcSize.Small and SKPathDirection.CounterClockwise
• magenta: SKPathArcSize.Large and SKPathDirection.CounterClockwise

If the tilted ellipse is not large enough to fit betwixt the ii points, then information technology is uniformly scaled until information technology is large plenty. Only two unique arcs connect the two points in that case. These can be distinguished with the SKPathDirection parameter.

Although this approach to defining an arc sounds complex on commencement meet, it is the simply approach that allows defining an arc with a rotated ellipse, and information technology is frequently the easiest approach when you need to integrate arcs with other parts of the contour.

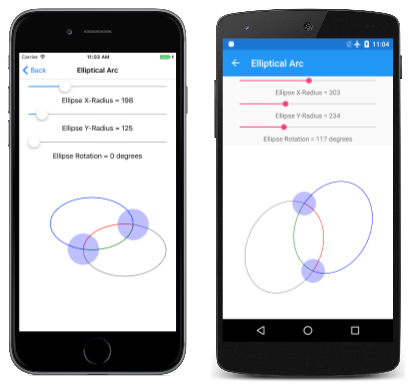
The Elliptical Arc page allows you to interactively prepare the two points, and the size and rotation of the ellipse. The EllipticalArcPage class derives from InteractivePage, and the PaintSurface handler in the EllipticalArcPage.xaml.cs lawmaking-behind file draws the iv arcs:

              void OnCanvasViewPaintSurface(object sender, SKPaintSurfaceEventArgs args) {     SKImageInfo info = args.Info;     SKSurface surface = args.Surface;     SKCanvas canvass = surface.Canvas;      sheet.Clear();      using (SKPath path = new SKPath())     {         int colorIndex = 0;         SKPoint ellipseSize = new SKPoint((float)xRadiusSlider.Value,                                           (float)yRadiusSlider.Value);         float rotation = (float)rotationSlider.Value;          foreach (SKPathArcSize arcSize in Enum.GetValues(typeof(SKPathArcSize)))             foreach (SKPathDirection direction in Enum.GetValues(typeof(SKPathDirection)))             {                 path.MoveTo(touchPoints[0].Center);                 path.ArcTo(ellipseSize, rotation,                            arcSize, direction,                            touchPoints[1].Center);                  strokePaint.Color = colors[colorIndex++];                 canvas.DrawPath(path, strokePaint);                 path.Reset();             }     }      foreach (TouchPoint touchPoint in touchPoints)     {         touchPoint.Paint(canvas);     } }                          

Here it is running:

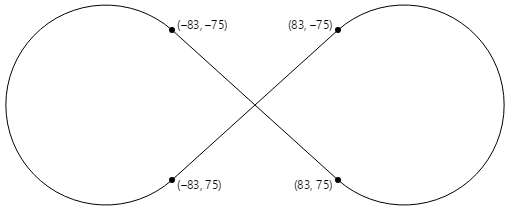
The Arc Infinity page uses the elliptical arc to depict an infinity sign. The infinity sign is based on 2 circles with radii of 100 units separated by 100 units:

Ii lines crossing each other are tangent to both circles:

The infinity sign is a combination of parts of these circles and the two lines. To use the elliptical arc to draw the infinity sign, the coordinates where the two lines are tangent to the circles must exist determined.

Construct a right rectangle in one of the circles:

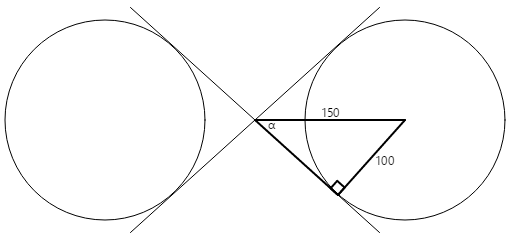
The radius of the circle is 100 units, and the hypotenuse of the triangle is 150 units, and so the bending α is the arcsine (inverse sine) of 100 divided by 150, or 41.8 degrees. The length of the other side of the triangle is 150 times the cosine of 41.eight degrees, or 112, which can too be calculated by the Pythagorean theorem.

The coordinates of the tangent point can then be calculated using this data:

x = 112·cos(41.8) = 83

y = 112·sin(41.8) = 75

The iv tangent points are all that'southward necessary to depict an infinity sign centered on the signal (0, 0) with circle radii of 100:

The PaintSurface handler in the ArcInfinityPage class positions the infinity sign and then that the (0, 0) point is positioned in the eye of the page, and scales the path to the screen size:

              void OnCanvasViewPaintSurface(object sender, SKPaintSurfaceEventArgs args) {     SKImageInfo info = args.Info;     SKSurface surface = args.Surface;     SKCanvas canvass = surface.Canvass;      canvas.Articulate();      using (SKPath path = new SKPath())     {         path.LineTo(83, 75);         path.ArcTo(100, 100, 0, SKPathArcSize.Large, SKPathDirection.CounterClockwise, 83, -75);         path.LineTo(-83, 75);         path.ArcTo(100, 100, 0, SKPathArcSize.Large, SKPathDirection.Clockwise, -83, -75);         path.Close();          // Use path.TightBounds for coordinates without control points         SKRect pathBounds = path.Premises;          canvas.Interpret(info.Width / 2, info.Superlative / 2);         canvas.Calibration(Math.Min(info.Width / pathBounds.Width,                               info.Meridian / pathBounds.Elevation));          using (SKPaint paint = new SKPaint())         {             paint.Manner = SKPaintStyle.Stroke;             paint.Color = SKColors.Bluish;             paint.StrokeWidth = five;              canvas.DrawPath(path, paint);         }     } }                          

The code uses the Bounds holding of SKPath to decide the dimensions of the infinity sine to calibration it to the size of the canvas:

The result seems a picayune small, which suggests that the Bounds property of SKPath is reporting a size larger than the path.

Internally, Skia approximates the arc using multiple quadratic Bézier curves. These curves (as you'll encounter in the next section) incorporate control points that govern how the bend is drawn but are not part of the rendered curve. The Premises property includes those control points.

To get a tighter fit, employ the TightBounds holding, which excludes the control points. Here'southward the program running in landscape mode, and using the TightBounds property to obtain the path bounds:

Although the connections between the arcs and straight lines are mathematically smooth, the change from arc to straight line might seem a picayune abrupt. A amend infinity sign is presented in the side by side commodity on Three Types of Bézier Curves.

• SkiaSharp APIs
• SkiaSharpFormsDemos (sample)

Feedback

Submit and view feedback for

harryfent1982.blogspot.com

Source: https://docs.microsoft.com/en-us/xamarin/xamarin-forms/user-interface/graphics/skiasharp/curves/arcs

Share this post